听说这个特性是很久以前了，总是读作「维拉迪克·坦普雷特」，一直没反应过来中文到底该叫什么，因为 C 时代的 Variadic Macro 我一直是很象形地读作「点点点」的 = =||

OK，扯远了。Variadic Template 对应中文应该是「可变参数模板」。

Parameter Pack

既然是可变参数，就需要通过某种方式来表示这些参数，而这里的解决方案就是 Parameter Pack 参数包，不知道可不可以简称「餐包」 =_,=

声明参数包的方法是在类型和名称之间加 ...：

template<typename... Types> struct Tuple {};
Tuple<>           t0;   // Types 中不含参数
Tuple<int>        t1;   // Types 中包含一个参数：int
Tuple<int, float> t2;   // Types 中包含两个参数：int 和 float

template<typename... Types> void f(Types... args);
f();        // args 中不包含参数
f(1);       // args 中包含一个参数：int(1)
f(2, 1.0);  // args 中包含两个参数：int(2) 和 double(1.0)

上面的两个示例中，Types 称作模板参数包，args 称作函数参数包。

参数包所包含的参数的个数可以用 sizeof... 取得。

Pack Expansion

既然提出了参数包，把所有可变参数容纳其中，那么就需要存在将其解包的操作。与 C 中 va_list 一个参数一个参数地手动解包不同，参数包的 Pack Expansion 是一口气将所有的参数以某种形式展开：

template<int... Entries>
struct IntArray {
    int array[sizeof...(Entries)] = { Entries... };
};

template<typename... Types> void bar(Types... args) {}
template<typename... Types> void foo(Types... args) {
    bar(&args...);
}

所谓「以某种形式」展开，就是将 pattern ... 转换为逗号分隔的 pattern_1, pattern_2, ... , pattern_N 的形式。从上面的函数 foo 就可以看出，传给 bar 的是各个参数的地址（没啥大意义）；即 void foo(a, b, c) 的 &args... 会展开成 &a, &b, &c。

std::tuple

作为一个可变参数模板的实际用例，C++11 还引入了 std::tuple 作为 std::pair 的推广形式（tuple 的意思即为元祖……哦不对，是元组……我是吃货我自重……），表示任意多个元素的组合。

使用 std::make_tuple 和 auto 可以很方便地声明一个元组：

auto x = std::make_tuple(3, 0.14, std::string("pie")); // std::tuple<int, double, std::string>

而对于各个元素的访问可以统一使用 std::get 实现（包括 std::array 和 std::pair 的大一统）：

auto element = std::get<2>(x);

另一个好玩的地方是使用 std::tie 创建 lvalue reference 的 tuple：

std::set<int> some_instance_of_std_set;
std::set<int>::iterator itr;
bool success;
std::tie(itr, success) = some_instance_of_std_set.insert(2012);

虽然看着有些丑陋，但似乎可以看到些「多返回值」的影子……

当然，也可以参照 Lua 中的 _ 使用 std::ignore 忽略多返回值中的特定位置的值：

int r1, r2;
std::tie(r1, std::ignore, r2) = std::make_tuple(3, 0.14, 4);

顺带的，既然是 lvalue reference，试图一句话交换两个变量的值是不可以全用 std::tie 的：

std::tie(a, b) = std::tie(b, a);        // 错误方式
std::tie(a, b) = std::make_tuple(b, a); // 正确方式

烫烫烫与屯屯屯

这两个乱码应该是不少 C/C++ 程序员的必经之路吧。

微软 Visual C++ 的 Debug 模式下，会为未初始化的内存填充一些初始值，以便调试。其中，栈上的内存都用 0xCC 初始化、堆上的内存都用 0xCD 初始化。

而如果把 0xCCCC 作为字符输出，在简体中文的 Windows 系统下，就会根据其使用的 GBK 编码将其解释为「烫」字；0xCDCD 则为「屯」。

变巨

如果你用过南极星，说明你已经老了。

在那个万码奔腾的年代，由于早年的《曹操传》和《三国志》等游戏使用的都是 Big5 编码的文本数据，而简体中文 Windows 系统使用的编码不同于 Big5。用「前朝的剑斩本朝的官」就产生了乱码。

「变巨」的 GBK 编码为 B1E4 BEDE（GB2312 亦然），而在 Big5 编码中这四个字节对应的汉字为「曹操」。

俸俸伲购美病

这是《英雄传说VI 空之轨迹SC》简体中文版中的一句对白，也是最初被玩家讽刺得最惨的地方。

打上官方修正补丁后可以发现原文为「嘿嘿嘿，还好啦。」之所以会产生这样的乱码是因为 GBK 编码：

BA D9 BA D9 BA D9 A3 AC BB B9 BA C3 C0 B2 A1 A3 // 嘿嘿嘿，还好啦。
   D9 BA D9 BA D9 A3 AC BB B9 BA C3 C0 B2 A1    // 俸俸伲购美病

缺了第一个字节……

锟斤拷

相对前面几个乱码的直白，这个乱码是很纠结的存在。

Unicode 中定义了一个特殊字符「�」即 U+FFFD，称作 Replacement Character。用来表示无法显示的字符或是无法解析的数据。

如果一段数据本身是使用 GBK 编码的，那么其中可能有很多部分不符合 UTF-8 编码规则。一个处理 UTF-8 数据的程序得到这段数据后，可以选择将数据中检测到不合 UTF-8 编码规则的部分替换为 UTF-8 编码的 U+FFFD 即 EFBFBD，这样，就在自动消除编码问题的同时对用户给出了数据编码错误的提示。

经过上面这步处理后，数据中就产生了很多 EFBFBD 的序列，此时如果试图以 GBK 将其解码，那么两个这样的序列就成了「锟斤拷」，即 EFBF BDEF BFBD。

我已经忘了上次备份服务器是什么时候的事了，只记得前不久因为「以为备份过」做错事然后手忙脚乱了。更考虑到自己邮箱那么多空间浪费着也是浪费着，于是就决定抽空写个脚本定期备份一下。

说是「自动」备份，其实一句话解释就是通过 cron 定期执行脚本，对需要备份的目录使用 tar 打包，然后 sendmail 发到邮箱。

这里的操作系统是 CentOS，其它系统应该也是大同小异。以下便是本次行动的流水帐 :)

Sendmail 相关

因为系统里原生没有安装 sendmail，于是

yum install sendmail   # 安装
service sendmail start # 启动服务
chkconfig sendmail on  # 开启自动启动

因为只想使用发信功能，所以也不用花时间改配置（收信功能的默认配置是只接受本地邮件）。确定防火墙允许 25 端口后，就可以使用下面的命令直接发送邮件了。

# 使用交互模式（使用只包含一个句点的行结束正文并发送）
mail <收件人>
# 命令行直接发送
echo <正文> | mail -s <主题> <发件人>

使用这种方法发出的邮件显示发件人地址为「<用户名>@<主机名称>」。因为 sendmail 只支持纯文本，所以需要借助 uuencode 来编码附件，于是：

# 只包含附件
uuencode <文件路径> <文件显示名称> | mail -s <主题> <收件人>
# 正文和附件
(echo <正文>; uuencode <文件路径> <文件显示名称>) | mail -s <主题> <收件人>

备份脚本

编写 Shell 脚本实现对 Web 目录的备份和发送工作，因为博客使用的是 SQLite 数据库，直接打包即可，不需要先用 mysqldump 导出。（新手上路，表示快被引号什么的弄疯了，于是大多数情况下都为变量加上了引号。另外邮件正文纯属无聊，完全可以不加 = =）

#!/bin/sh

# 备份文件存放目录
BACKUP_DIR="/path/to/backup/directory"

# 备份文件邮件接收地址
BACKUP_MAIL_RECEIVER="example@example.com"

# =====================================

# 保证目录存在
[ ! -d "$BACKUP_DIR" ] &&  mkdir -p "$BACKUP_DIR"

# 需要备份的路径
WEB_DIR="/path/to/web/root"

BACKUP_DATE="`date +%Y-%m-%d`"

BACKUP_FILE_NAME="$BACKUP_DATE.tar.gz"
BACKUP_FILE_FULLNAME="$BACKUP_DIR/$BACKUP_FILE_NAME"

cd $WEB_DIR
    tar czpf "$BACKUP_FILE_FULLNAME" *

BACKUP_MAIL_SUBJECT="VPS Backup: $BACKUP_DATE"
BACKUP_MAIL_MESSAGE=$(
    echo "Sir,";
    echo "";
    echo "Backup file $BACKUP_FILE_FULLNAME created.";
)

(echo "$BACKUP_MAIL_MESSAGE"; uuencode "$BACKUP_FILE_FULLNAME" "$BACKUP_FILE_NAME") \
    | mail -s "$BACKUP_MAIL_SUBJECT" "$BACKUP_MAIL_RECEIVER"

保存后给脚本加上执行权限，就可以直接运行试一下，应该会有邮件发到邮箱了。

chmod u+x <脚本名>

定时执行

定时执行肯定就是 cron 了，这个不用多说，直接 crontab -e 然后添加一行：

0 0 * * 2 /path/to/script

就大功告成鸟～从此，每周二午夜就会有一封谜之信件安静地躺到你的邮箱里……

协程（coroutine）并不是 Lua 独有的概念，如果让我用一句话概括，那么大概就是：一种能够在运行途中主动中断，并且能够从中断处恢复运行的特殊函数。（嗯，其实不是函数。）

举个最原始的栗子

下面给出一个最简单的 Lua 中 coroutine 的用法演示：

function greet()
    print "hello world"
end

co = coroutine.create(greet) -- 创建 coroutine

print(coroutine.status(co))  -- 输出 suspended
print(coroutine.resume(co))  -- 输出 hello world
                             -- 输出 true (resume 的返回值)
print(coroutine.status(co))  -- 输出 dead
print(coroutine.resume(co))  -- 输出 false    cannot resume dead coroutine (resume 的返回值)
print(type(co))              -- 输出 thread

协程在创建时，需要把协程体函数传递给创建函数 create()。新创建的协程处于 suspended 状态，可以使用 resume 让其运行，全部执行完成后协程处于 dead 状态。如果尝试 resume 一个 dead 状态的，则可以从 resume 返回值上看出执行失败。另外你还可以注意到 Lua 中协程（coroutine）的变量类型其实叫做「thread」Orz...

乍一看可能感觉和线程没什么两样，但需要注意的是 resume() 只有在 greet() 以某种形式「返回」后才会返回（所以说协程像函数）。

函数执行的中断与再开

单从上面这个例子，我们似乎可以得出结论：协程果然就是某种坑爹的函数调用方式啊。然而，协程的真正魅力来自于 resume 和 yield 这对好基友之间的羁绊。

函数 coroutine.resume(co[, val1, ...])

开始或恢复执行协程 co。

如果是开始执行，val1 及之后的值都作为参数传递给协程体函数；如果是恢复执行，val1 及之后的值都作为 yield() 的返回值传递。

第一个返回值（还记得 Lua 可以返回多个值吗？）为表示执行成功与否的布尔值。如果成功，之后的返回值是 yield 的参数；如果失败，第二个返回值为失败的原因（Lua 的很多函数都采用这种错误处理方式）。

当然，如果是协程体函数执行完毕 return 而不是 yield()，那么 resume() 第一个返回值后跟着的就是其返回值。

函数 coroutine.yield(...)

中断协程的执行，使得开启该协程的 coroutine.resume() 返回。再度调用 coroutine.resume() 时，会从该 yield() 处恢复执行。

当然，yield() 的所有参数都会作为 resume() 第一个返回值后的返回值返回。

OK，总结一下：当 co = coroutine.create(f) 时，yield() 和 resume() 的关系如下图：

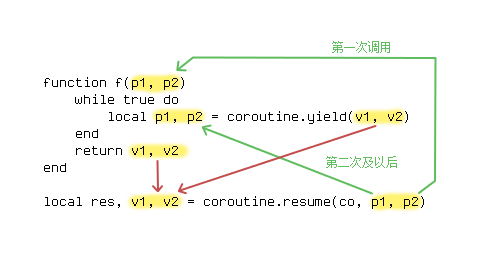
How coroutine makes life easier

如果要求给某个怪写一个 AI：先向右走 30 帧，然后只要玩家进入视野就往反方向逃 15 帧。该怎么写？

传统做法

经典的纯状态机做法。

-- 每帧的逻辑
function Monster:frame()
    self:state_func()
    self.state_frame_count = self.state_frame_count + 1
end

-- 切换状态
function Monster:set_next_state(state)
    self.state_func = state
    self.state_frame_count = 0
end

-- 首先向右走 30 帧
function Monster:state_walk_1()
    local frame = self.state_frame_count
    self:walk(DIRECTION_RIGHT)
    if frame > 30 then
        self:set_next_state(state_wait_for_player)
    end
end

-- 等待玩家进入视野
function Monster:state_wait_for_player()
    if self:get_distance(player) < self.range then
        self.direction = -self:get_direction_to(player)
        self:set_next_state(state_walk_2)
    end
end

-- 向反方向走 15 帧
function Monster:state_walk_2()
    local frame = self.state_frame_count;
    self:walk(self.direction)
    if frame > 15 then
        self:set_next_state(state_wait_for_player)
    end
end

协程做法

-- 每帧的逻辑
function Monster:frame()
    -- 首先向右走 30 帧
    for i = 1, 30 do
        self:walk(DIRECTION_RIGHT)
        self:wait()
    end

    while true do
        -- 等待玩家进入视野
        while self:get_distance(player) >= self.range do
            self:wait()
        end

        -- 向反方向走 15 帧
        self.direction = -self:get_direction_to(player)
        for i = 1, 15 do
            self:walk(self.direction)
            self:wait()
        end
    end
end

-- 该帧结束
function Monster:wait()
    coroutine.yield()
end

额外说一句，从 wait() 函数可以看出，Lua 的协程并不要求一定要从协程体函数中调用 yield()，这是和 Python 的一个区别。

字符画版本的 Bad Apple 的流行应该是好多年以前的事情了吧……虽然当时也想过自己做一个，但一直觉得图片转字符画是一个很神秘的过程（据说 mplayer 可以直接把视频按字符画输出）。前两天做完 ssoaag 发现，貌似可以用这个东西的原理输出字符动画，于是就有了下面这个视频 = =

【似乎是教程】如何制作字符动画

看到最后的效果你会发现最终产出的字符动画最右一列字符是略有问题的，在视频里也注明了，是那个 GetColor 函数里有个失误 = = 会导致某些情况下取到下一行的颜色，需要 continue 掉，并且把最后除以的 w * h 变成真正有效的像素数。